数据结构与算法（三）—— 线性表的应用

数据结构笔记目录：

1. 数据结构与算法（一）—— 线性表的顺序表示及常用操作
2. 数据结构与算法（二）—— 线性表的链式表示及常用操作
3. 数据结构与算法（三）—— 线性表的应用
4. 数据结构与算法（四）—— 栈和队列
5. 数据结构与算法（五）—— 串、数组和广义表
6. 数据结构与算法（六）—— 数和二叉树

循环链表

循环链表的合并

LinkList Connect(LinkList Ta,LinkList Tb){ //传入两个循环链表的尾指针，本操作为返回一个新表，故无需使用引用类型（&）进行传参
    Nnode* p = Ta -> next; //p存储表头结点
    Ta -> next = Tb -> next -> next; //Ta表尾的next指向Tb首元结点
    free(Tb -> next); //释放Tb头结点
    Tb -> next = p; //Tb的next指向Ta表头结点
    return Tb; //返回修改后的循环链表尾指针
 }

双向链表

双向链表的定义

typedef struct DuLNode{
   Elemtype data;
   struct DuLNode* prior;
   struct DLNode* next;
}DuLNode,*DuLinkList;

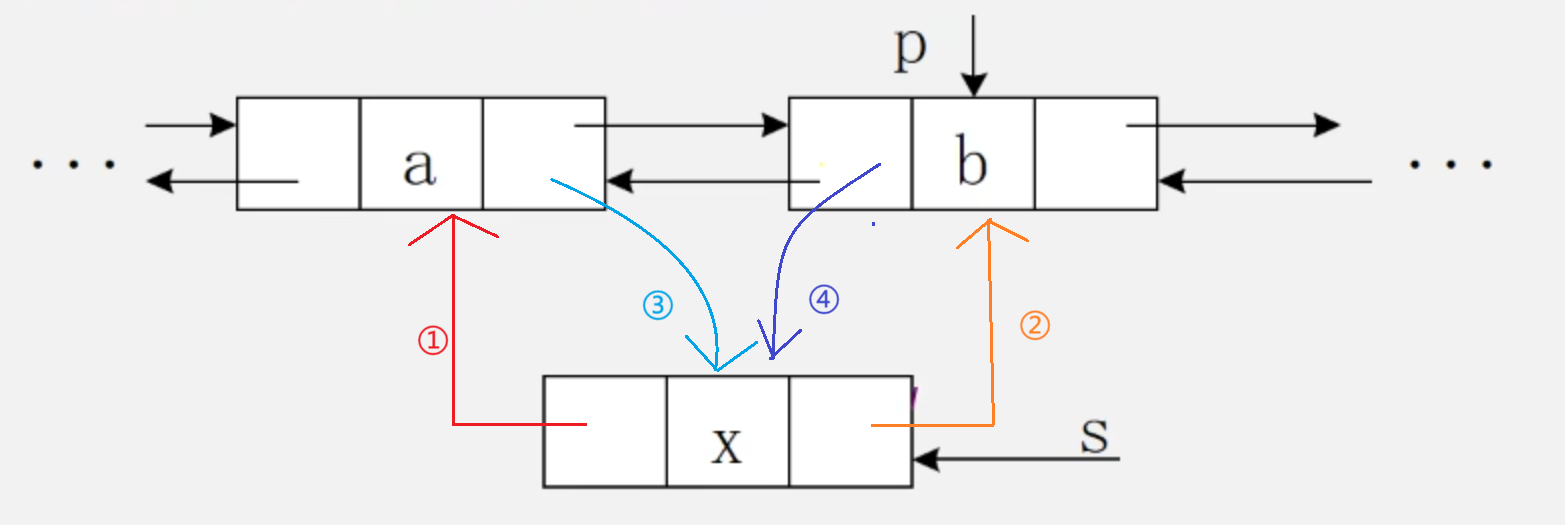
双向链表的插入

int ListInsert_Dul(DuLinkList &L,int i,ElemType e){
   if(!(p=GetElemP_Dul(L,i))) return 0;
   DuLNode* s = (DuLNode*)malloc(sizeof(DuLNode)); 
   s -> data = e; //为要插入的s结点分配空间
   s -> prior = p -> prior;
   s -> next = p; //设置要插入节点的前驱和后继
   /* 这一步我这样处理是因为首先进行这两步不会影响原表的结构，便于理解 */
   (p -> prior) -> next = s; //p -> prior 即为a结点，设置a结点的后继为s
   p -> prior = s; //p结点指向b结点，设置b结点的前驱为s
   return 1;
}   

双向链表的删除

int ListDelete_DuL(DuLinkList &L,int i,ElemType &e){
   if(!(p=GetElemP_Dul(L,i))) return 0;
   e = p -> data;
   (p -> next) -> prior = p -> prior; //p -> next 为p的后继结点，设置此结点前驱域为p的前驱
   (p -> prior) -> next = p -> next; //p -> prior 为p的前驱结点，设置此结点后继域为p的后继
   free(p); //释放要删除的节点
   return 1;
}   

单链表、循环链表和双向链表的时间效率比较

	查找表头结点（首元结点）	查找表尾结点	查找结点*P的前驱结点
带头结点的单链表L	L -> next 时间复杂度O(1)	从L -> next依次向后遍历 时间复杂度O(n)	通过p -> next无法找到其前驱
带头结点的仅设头指针L的循环单链表	L -> next 时间复杂度O(1)	从L -> next依次向后遍历 时间复杂度O(n)	通过p -> next可以找到其前驱 时间复杂度O(n)
带头结点的仅设尾指针R的循环单链表	R -> next -> next 时间复杂度O(1)	R 时间复杂度O(1)	通过p -> next可以找到其前驱 时间复杂度O(n)
带头结点的双向循环链表L	L -> next 时间复杂度O(1)	L -> prior 时间复杂度O(1)	通过p -> prior 时间复杂度O(1)

顺序表和链表的比较

链表的优缺点

优点：

1. 结点空间可以动态申请和释放
2. 插入和删除时不需要移动数据元素

缺点：

1. 存储密度小，每个结点的指针域会占用额外的存储空间
2. $存储密度 = \frac{结点数据本身占用的空间}{结点占用的空间总量}$（即$\frac{数据域所占空间}{数据域所占空间+指针域所占空间}$）（顺序表的存储密度为1）
3. 链式存储结构是非随机存取结构，对任一结点的操作都要从头指针依指针链查找到该节点

适用情况

1. 表长变化较大
2. 频繁进行插入或删除操作

顺序表的优缺点

优点：

1. 存储密度为1，不用为表示结点间逻辑结构增加而外的存储开销
2. 随机存取，按位置访问元素的时间复杂度为O（1）

缺点：

1. 结点空间预先分配，可能会导致闲置或溢出
2. 插入和删除时平均约移动表中一半元素，时间复杂度O(n)

适用情况

1. 表长变化不大，且能事先确定变化范围
2. 很少进行插入或删除操作，经常按元素位置序号访问数据元素

线性表的应用

线性表的合并（将Lb表插入到La表后）

void union(List &La,List &Lb){
   La_Len = ListLength(La);
   Lb_Len = ListLength(Lb);
   for(i = 1,i <= Lb_Len.i++){
      GetElem(i,Lb,e); //获得Lb的第i个元素
      if(!LocateElem(La,e)) ListInsert(&La,e,La_Len++); //检查La中有无e元素，如果没有，则将e元素插入到La表尾
   }

}

算法的时间复杂度为：O(ListLength(La) * ListLength(Lb))

有序表的合并（顺序表实现）

void MergeList_Sq(SqList LA,SqList LB,SqList &LC){
   int* pa = LA.elem;
   int* pb = LB.elem; //指针pa和pb分别指向两个顺序表首元素
   LC.length = LA.length + LB.length; //信标长度为两表长度和
   LC.elem = (int *)malloc(sizeof(int) *max_Size); //为合并后的新表分配空间
   int* pc = LC.elem;  //指针pc指向LC表首元素
   int* pa_Last = LA.elem + LA.lenght - 1; 
   int* pb_Last = LB.elem + LB.lenght - 1; //pa_Last,pb_Last 分别指向LA，LB两表最后一个元素
   while(pa <= pa_Last && pb <= pb_Last){ //循环条件为两表未到达表尾
      if(*pa >= *pb) *pc++ = *pb++; //可写为{*pc = *pb;pc++;pb++;}
      else *pc++ = *pa++; //可写为{*pc = *pa;*pc++;*pa++;}
      /*由于C/C++的运算符优先级规则，赋值运算符（=）的优先级低于后缀递增运算符（++），但是，后缀递增运算符的操作顺序为：先使用（或赋值）当前值，再进行递增操作。 */
   }
      while(pa <= pa_Last)*pc++ = *pa++;
      while(pa <= pa_Last)*pc++ = *pb++; //将未到达末尾的表中剩余元素添加至LC表表尾
}

有序表的合并（链表实现）

void MergeList_L(LinkList LA,LinkList LB,LinkList &LC){
   LNode* p = LA -> next;LNode* q = LB -> next;
   LNode* r = LC = LA; //用LA头结点做LC头结点，目的是将LB表整合到LA表
   /*p表示LA链表访问到的最后一个位置，q表示LB链表访问到的最后一个位置，r表示LC链表当前的最后一个节点*/
   while(p  != NULL && q != NULL){
      if(p -> data >= q -> data){
         r -> next = q; 
         r = q;
         q = q -> next;
      }
      else{
         r -> next = p;
         r = p;
         p = p -> next;
      }
      r -> next  =  p ? p : q; //p如果非空，则将p赋值给 r -> next,否则将q赋值给r -> next
      /*这一步的目的是将未访问到最后一个结点的表插入到LC表末尾，*/
      free(LB); //释放LB头结点
   }
}

综合应用案例

稀疏多项式的运算（完整实现）

typedef struct PNode{
float coef; //系数
int expn; //指数
struct PNode* next; //指针域
}PNode,*Polynomal;
typedef struct PNode{
float coef; //系数
int expn; //指数
struct PNode* next; //指针域
}PNode,*Polynomal;
void MergeList_L(Polynomal LA,Polynomal LB,Polynomal &LC){
   	PNode* p = LA -> next;PNode* q = LB -> next; //p,q指针指向LA,LB两表首元素
   	PNode* r = LC; //r指向LC表
   	while(p != NULL && q != NULL){  //循环条件为LA,LB两表均未到达表尾
    	if(p -> expn == q -> expn){ //第一层if：p，q指数相等情况
      		if(p -> coef + q -> coef == 0){ //第二层if：判断p，q系数是否相加为零
      		p = p -> next;
      		q = q -> next; //系数和为零，向后移动p，q指针，两结点均不加入LC表
        	continue;
      		}
      		else{ //第二层if：p，q系数相加不为零
        		PNode* s = (PNode*)malloc(sizeof(PNode));
        		s -> next = NULL; //初始化一个s结点以便插入LC表
        		s -> coef =  p -> coef + q -> coef;
        		s -> expn = p -> expn; //新结点指数为p（或q）指数，系数为p，q系数之和
        		r -> next = s; //将s结点插入LC表
        		r = r -> next;
        		p = p -> next;
      		q = q -> next; //向后移动p，q，r指针
      		}
    	}
    	else if(p -> expn < q -> expn){ //第一层if：p指数小于q指数
        	r -> next = p;
        	p = p -> next;
        	r = r -> next; //将p所指向结点作为r的下一个结点
    	}
    	else{ //第一层if：p指数大于q指数
        	r -> next = q;
        	q = q -> next;
        	r = r -> next; //将q所指向结点作为r的下一个结点
    	}
 }
	r -> next = p ? p : q; //p如果非空，则将p赋值给 r -> next,否则将q赋值给r -> next
   /*这一步的目的是将未访问到最后一个结点的表插入到LC表末尾，*/
}