数据结构与算法（四）—— 栈和队列

数据结构笔记目录：

1. 数据结构与算法（一）—— 线性表的顺序表示及常用操作
2. 数据结构与算法（二）—— 线性表的链式表示及常用操作
3. 数据结构与算法（三）—— 线性表的应用
4. 数据结构与算法（四）—— 栈和队列
5. 数据结构与算法（五）—— 串、数组和广义表
6. 数据结构与算法（六）—— 数和二叉树

栈与队列的应用实例

出栈顺序

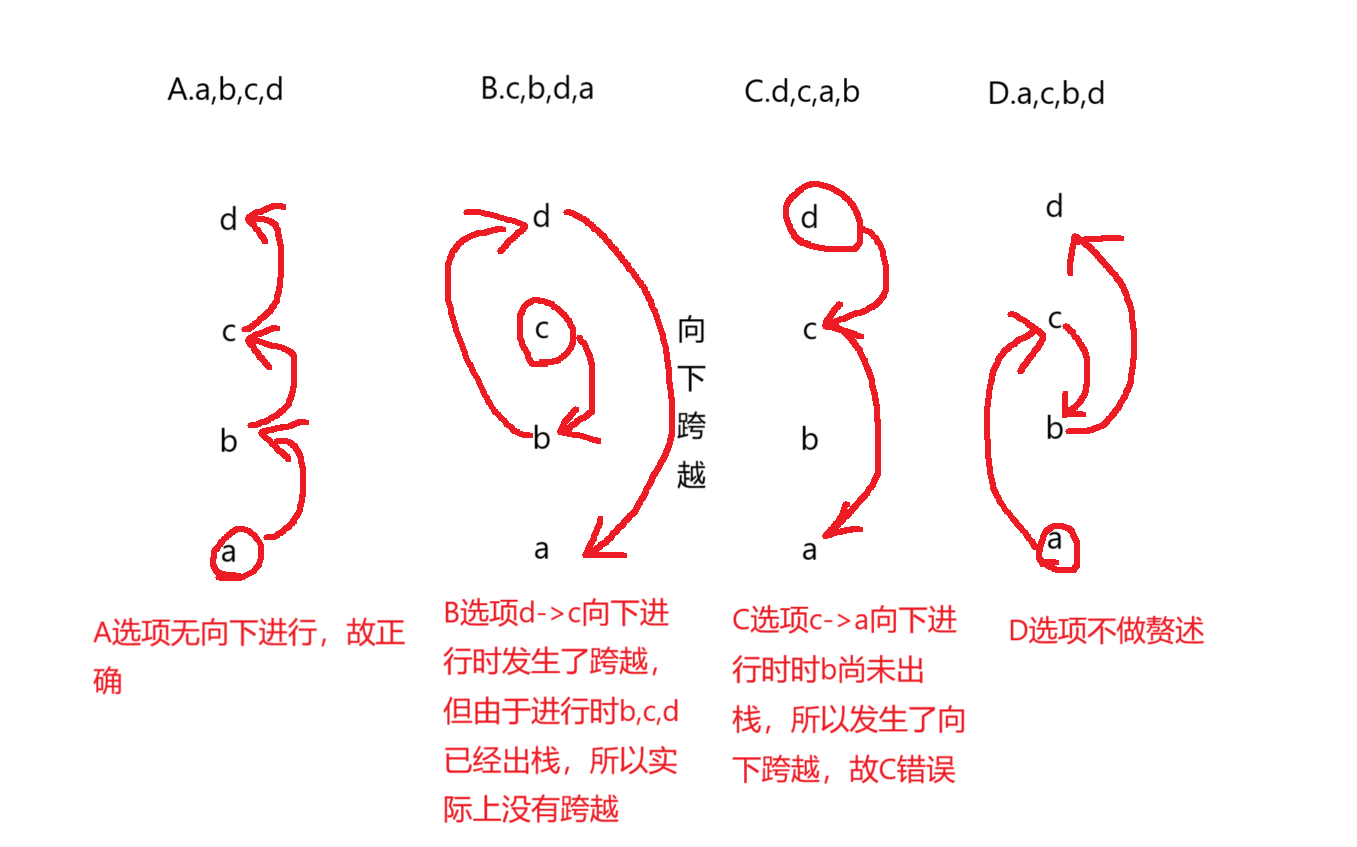
• 条件: 进栈时允许出栈
• 解题思路: 向上进行时可以跳跃，向下进行时不可以出现跳跃

Ex:1

某栈的输入序列为a,b,c,d，下面的四个序列中，不可能为其输出序列的是（）
A.a,b,c,d    B.c,b,d,a    C.d,c,a,b    D.a,c,b,d

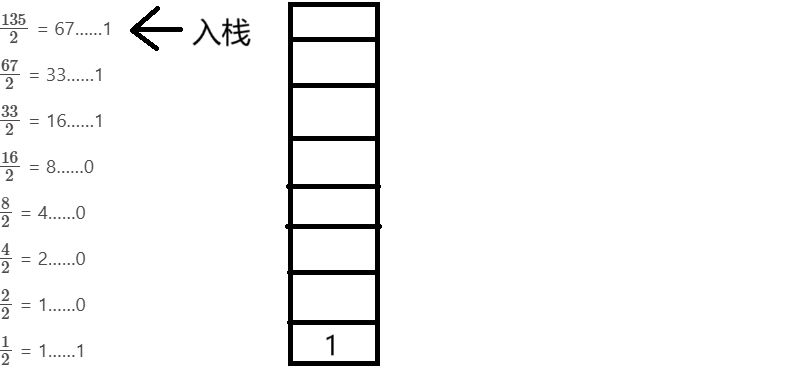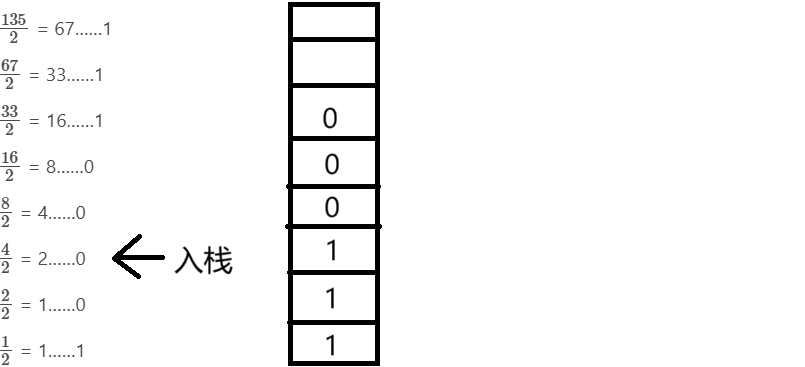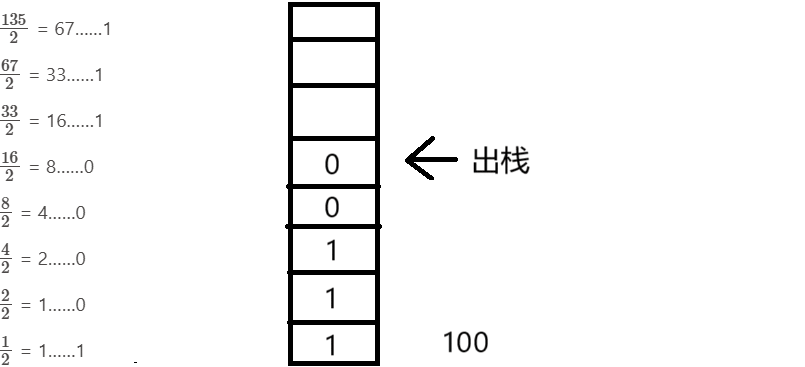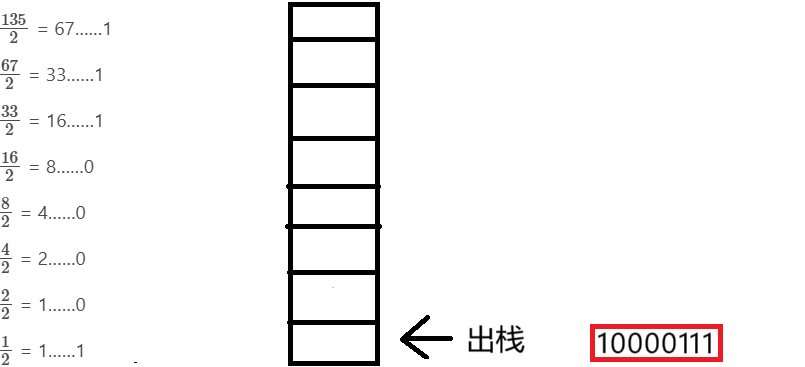
进制转换：倒取n/d的余数（d为进制数）

EX:2：取 135的二进制数（完整实现）

括号匹配的检验

依次压入所求括号，遇到右括号便进行出栈操作两次，如果两括号匹配则继续进行入栈和遇到右括号便出栈两次的操作，如果不匹配则退出循环返回括号不匹配

顺序栈的初始化、判空、清空、求长、销毁

顺序栈的表示

#define max_Size 100
typedef struct SqStack{
    ElemType* base; //栈底指针
    ElemType* top;  //栈顶指针
    int stacksize;  // 栈的最大容量
}SqStack;

顺序栈的初始化

int InitStack(SqStack &S){
    S.base = (ElemType *)malloc(sizeof(ElemType)*max_Size);
    if(!S.base) return 0; //分配内存失败，返回0
    S.top = S.base; //栈底指针等于栈顶指针，判断栈空的条件
    return 1；
}

顺序栈的判空

int StackEmpty(SqStack &S){
    if(S.top==S.base) return 1;
    else return 0;
}

清空顺序栈

int ClearStack(SqStack &S){
    if(S.base) S.top = S.base; //并不需要全部释放，只需栈底指针等于栈顶指针（满足栈空条件）即可
    return 1;
}

求顺序栈长度

int StackLength(SqStack S){
    return 1;
    return S.top - S.base;
}

销毁顺序栈

int DestroyStack(SqStack &S){
    if(S.base){
        free(S.base); //S.base是一块包含栈所有元素的空间
        S.stacksize = 0;
        S.top = S.base = NULL;
    } 
}

顺序栈的入栈与出栈

入栈

int Push(SqStack &S,ElemType e){
    if(S.top - S.base == S.stacksize) return 0; //判断是否栈满，如果栈满则返回溢出
    *S.top = e; //解引用S所指的地址，将e压入栈
    S.top++; //栈顶上移
    return 1;
}

出栈

int Pop(SqStack &S,ElemType &e){
    if(S.top == S.base) return 0; //判断是否为空栈，如果为空栈则返回溢出
    S.top--; //先进行栈顶下移
    e = *S.top; //后进行解引用S所指的地址，存入e
    return 1;
}

应用：十进制转换二进制数

#include <iostream>
#include <cstdlib>
using namespace std;
#define max_Size 100
typedef struct SqStack{
	int* top = NULL;
	int* base = NULL;
	int stacksize = max_Size;
}SqStack;
int Push(SqStack &S,int e){
	if(S.top - S.base == S.stacksize) return 0;
	*S.top = e;
	S.top++;
	return 1;
}

int Pop(SqStack &S){
	if(S.top == S.base) return 0;
	S.top--;
	int t = *S.top;
	return t;
}

int main(){
	SqStack S;
	S.base = (int *)malloc(sizeof(int)*max_Size);
	S.top = S.base;
	int x;
	cin >> x;
	while(x>0){
		int t = x%2;
		Push(S,x%2);
		x = (x - t)/2;
	}
	while(S.top != S.base) cout << Pop(S);
	
}

链栈的初始化、判空

链栈的初始化

void InitStack(LinkStack &S){
    S = NULL;
}

节点定义

typedef struct StackNode{
    Elemtype data;
    StackNode* next;
}StackNode,*LinkStack;

链栈的判空

int StackEmpty(LinkStack &S){
    if(S == NULL) return 1; //链栈为空
    else return 0;
}

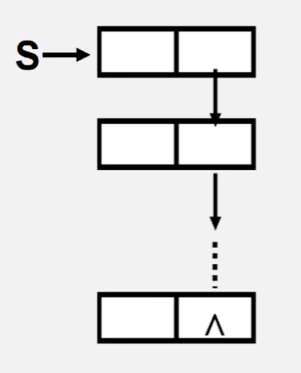
链栈的出入栈操作

与普通链表不同，链栈是一个不带头结点的链表，链栈指针S指向的是链表末尾元素（因为链表后进先出的特性）
如图所示：

链栈的入栈

int push(LinkStack &S,Elemtype e){
    StackNode* p = (StackNode *)malloc(sizeof(StackNode));
    p -> data = e; //创建要插入的新结点p
    p -> next = S; 
    S = p; //上移栈顶
    return 1;
}

链栈的出栈

int pop(LinkStack &S,Elemtype &e){
    if (S==NULL) return 0; //如果传入的链栈为空栈，返回溢出
    e = S -> data; //存储被释放的结点的数据
    StackNode* p = S; //生成临时结点p用于存放被释放的S结点地址
    S = S -> next; //下移栈顶
    free(p); //释放指针
    return 1;
}

队列的真溢出、假溢出

真溢出：front==0;rear==max_Size
假溢出：front！=0;rear==max_Size
由于假溢出的存在，大部分队列使用的是顺序循环结构

队列的表示、入队、出队

队列的表示

typedef struct SqQueue{
    ElemType* base; //初始化动态分配存储空间
    int front; //队头下标
    int rear; //队尾下标
}

队列的入队

Q.base[Q.rear] = x;
Q.rear = (Q.rear + 1) % max_Size;

队列的出队

x = Q.base[Q.front];
Q.front = (Q.front + 1) % max_Size;

注意：

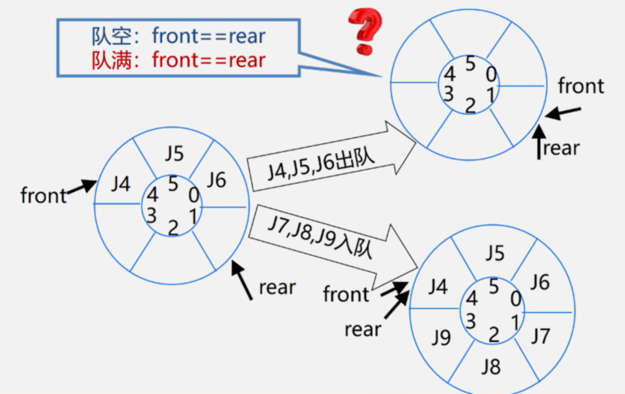
1. 循环队列并非是一个真正的循环结构，而是通过取余（%）运算来实现循环。
2. 循环队列无法判断队空、队满，二者条件均为rear==front，如图所示：
   

解决方案：

1. 另外设一个标志以区别队空队满
2. 另设一个变量记录元素个数
3. 少用一个元素空间

基于少用一个空间的区分循环队列队满队空的方法

(Q.rear + 1) % max_Size =   Q.front; //队尾指针 +1 等于队头指针时证明队满
Q.rear == Q.front; //队尾指针等于队头指针时证明队空

队列的初始化、求长

队列的初始化

int InitQueue(SqQueue &Q){
    Q.base = (ElemType *)malloc(sizeof(ElemType) * max_Size); //分配空间
    if(!Q.base) return 0;
    Q.front = Q.rear = 0;  //队头队尾指针初始化为0
    return 1;
}

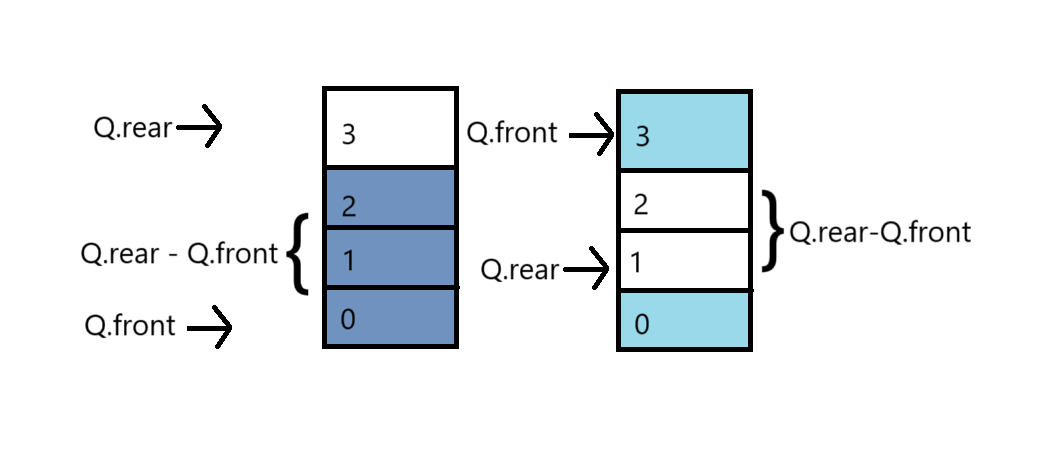
队列求长

int QueueLength(SqQueue Q){
    return (Q.rear-Q.front + max_Size) % max_Size;
}

队列的入队、出队

队列的入队

int EnQueue(SqQueue &Q,ElemType e){
    if((Q.rear + 1) % max_Size == Q.front) return 0; //队满，返回错误
    Q.base[Q.rear] = e; //队尾插入新元素
    Q.rear = (Q.rear + 1) % max_Size; //队尾指针+1
}

队列的出队

int DeQueue(SqQueue &Q,ElemType &e){
    if(Q.rear == Q.front) return 0; //队空，返回错误
    e = Q.base[Q.front]; //将队头出队元素赋值给e
    Q.front = (Q.front + 1) % max_Size; //队头指针+1
}

链队列相关操作

链队列定义

typedef struct QNode{
    ElemType data;
    Qnode* next;
}QNode,*QueuePtr;
typedef struct LinkQueue{
    QNode* front; //队头指针
    QNode* rear; //队尾指针
}LinkQueue; //把两个指针合成一个结构体看起来更简洁。

链队列初始化

int InitQueue(LinkQueue &Q){
    Q.rear = Q.front = (QNode *)mallco(sizeof(QNode));
    Q.front -> next = NULL;
    return 1;
}

链队列销毁

int DestroyQueue(LinkQueue &Q){ 
    while(Q.front!= NULL){
        QNode* p = Q.front;
        Q.front = Q.front -> next;
        free(p);
    } 
    Q.rear = NULL;
    return 1;
}

链队列入队

int EnQueue(LinkQueue &Q,ElemType e){
    QNode* p = (QNode *)mallco(sizeof(QNode));
    p -> data = e;
    p -> next = NULL; //创建要入队的结点
    Q.rear -> next = p; //入队
    Q.rear = p; //尾指针后移
}

链队列出队

int EnQueue(LinkQueue &Q,ElemType &e){
    if(Q.rear = Q.front) return 0; //空队列时返回0
    QNode* p = Q.front -> next; //p指向要出队元素
    e = p -> data; //将出队元素记录给e
    Q.front -> next = p -> next; //front指针后移
    if(Q.rear == p) Q.rear = Q.front; //尾指针元素已出队，此时队列只剩头结点，即空队列。此时Q.rear为空。故人为满足空表条件：Q.rear = Q.front;
    free(p); //释放p
    
}