数据结构与算法（五）—— 串、数组和广义表
串的模式匹配：BF算法
串的定义
1 |
|
DF算法
1 | int index_BF(SString A,SString B){ |
主函数内容
1 | int main(){ |
串的模式匹配：KMP算法
求next数组
一个讲的通俗易懂的课：KMP算法
步骤：
- 找到ch[n]位置前的最长公共前后缀，记录串长n，(n+1)为此位置next值
- CH[1]的next规定为0
求nextval数组
将ch[i]与ch[next[i]]比较。不相等，则nextval[i] = next[i];相等，则nextval[i] = next[next[i]]。
特殊矩阵压缩存储
对称矩阵/三角矩阵
以行序为主序：
$对角矩阵数组下三角部分[k]= \frac{(i-1)*(1+(i-1))}{2} + (j-1)$
上三角部分交换i，j即可
对于三角矩阵：
$下三角矩阵[k]= \frac{(i-1)*(1+(i-1))}{2} + (j-1)$
$上三角矩阵[k]= \frac{n*(n+(n-(i-1)+1))}{2} + (j-1)$
注意：三角矩阵需要额外一个存储常数c的位置
$k= \frac{n*(1+n)}{2} + 1$
稀疏矩阵：非零元素<=5%的矩阵
有序的双下标法
由三元组{(row,col,$a_{ij}$)}和矩阵维数(row,col)表示
通常在三元组下标为0的位置存放总行数，总列数，总非零元素个数等信息。
- 优点：非零元在表中按行序有序存储，因此便于进行依行顺序处理的矩阵运算
- 缺点：不能随机存取，若按行号取某一行中的非零元，则需从头开始查找
十字链表法
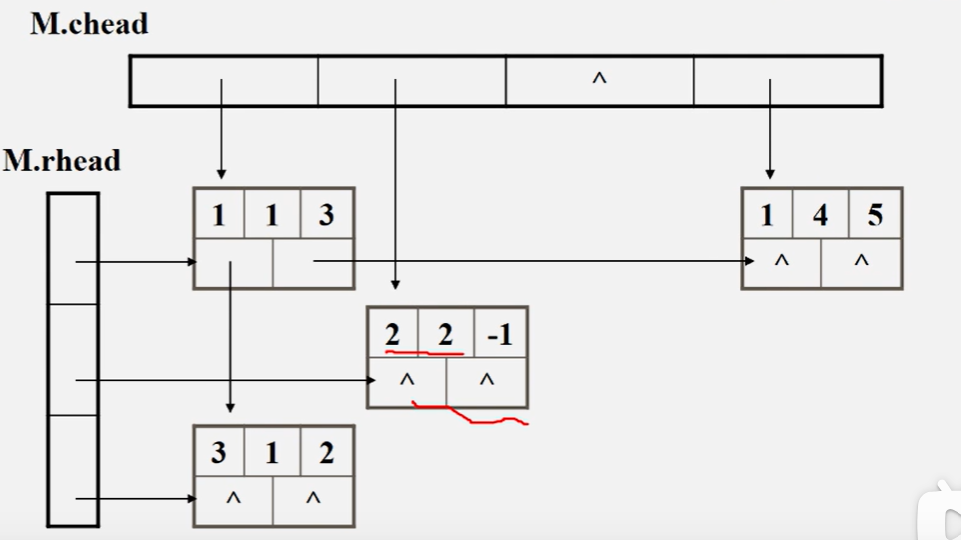
广义表
- 取表头：取第一个元素
- 取表尾：取除了第一个元素外其他元素组成的表
- 求表长：所包含元素个数（最外层逗号间隔出的元素个数）
- 求表深：最大的括号层数
本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 HaruYuki's Blog！
相关推荐
2025-01-24
数据结构与算法（三）—— 线性表的应用
数据结构笔记目录：数据结构与算法（一）—— 线性表的顺序表示及常用操作数据结构与算法（二）—— 线性表的链式表示及常用操作数据结构与算法（三）—— 线性表的应用数据结构与算法（四）—— 栈和队列数据结构与算法（五）—— 串、数组和广义表数据结构与算法（六）—— 数和二叉树 循环链表循环链表的合并 1234567LinkList Connect(LinkList Ta,LinkList Tb){ //传入两个循环链表的尾指针，本操作为返回一个新表，故无需使用引用类型（&）进行传参 Nnode* p = Ta -> next; //p存储表头结点 Ta -> next = Tb -> next -> next; //Ta表尾的next指向Tb首元结点 free(Tb -> next); //释放Tb头结点 Tb -> next = p; //Tb的next指向Ta表头结点 return Tb; //返回修改后的循环链表尾指针 } 双向链表双向链表的定义 12345typedef...
2025-02-09
数据结构与算法（四）—— 栈和队列
数据结构笔记目录：数据结构与算法（一）—— 线性表的顺序表示及常用操作数据结构与算法（二）—— 线性表的链式表示及常用操作数据结构与算法（三）—— 线性表的应用数据结构与算法（四）—— 栈和队列数据结构与算法（五）—— 串、数组和广义表数据结构与算法（六）—— 数和二叉树 栈与队列的应用实例出栈顺序 条件: 进栈时允许出栈 解题思路: 向上进行时可以跳跃，向下进行时不可以出现跳跃 Ex:1某栈的输入序列为a,b,c,d，下面的四个序列中，不可能为其输出序列的是（）A.a,b,c,d B.c,b,d,a C.d,c,a,b D.a,c,b,d 进制转换：倒取n/d的余数（d为进制数）EX:2：取...
2025-03-04
数据结构与算法（六）—— 数和二叉树
数据结构笔记目录：数据结构与算法（一）—— 线性表的顺序表示及常用操作数据结构与算法（二）—— 线性表的链式表示及常用操作数据结构与算法（三）—— 线性表的应用数据结构与算法（四）—— 栈和队列数据结构与算法（五）—— 串、数组和广义表数据结构与算法（六）—— 数和二叉树 树的相关定义 根节点：非空树中无前驱结点的结点 结点的度：结点拥有的子树数量 树的度：树内各节点的最大度 叶子：度等于零的终端节点 孩子与双亲：结点的子树的根称为该结点的孩子，该结点称为孩子的双亲 祖先：从根到该结点所经分支上的所有结点 有序树：将树中每个结点的各子树看成是从左到右有次序的(即不能互换) 无序树：将树中每个结点的各子树从左到右是没有次序的(即可以互换) 二叉树的性质 在二叉树的第i层上至多有$2^{i-1}$个结点 深度为k的二叉树至多有$2^{k}-1$个结点 对于任何一颗二叉树T，如果其叶子数为$n_{0}$，度为2的结点数为$n_{2}$，则$n_{0} = n_{2} +1$对于完全二叉树： 具有n个结点的完全二叉树的深度为$\lfloor log_2(n)...
2025-01-13
数据结构与算法（二）—— 线性表的链式表示及常用操作
数据结构笔记目录：数据结构与算法（一）—— 线性表的顺序表示及常用操作数据结构与算法（二）—— 线性表的链式表示及常用操作数据结构与算法（三）—— 线性表的应用数据结构与算法（四）—— 栈和队列数据结构与算法（五）—— 串、数组和广义表数据结构与算法（六）—— 数和二叉树 单链表的表示123456789typedef struct Lnode{ ElemType data; struct Lnode* next;}Lnode,*LinkList; //LinkList为指向结构体Lnode的指针类型//定义链表LinkList L;//定义节点指针pLNode* p;//LinkList == LNode*，分开两种定义方式的目的是使定义更加清晰 Ex:1：存储学生信息的单链表123456typedef struct student{ char nom[12]; //学号数据域 char name[8]; //姓名数据域 int score; //学生成绩数据域 struct student* next;...
2025-01-13
数据结构与算法（一）—— 线性表的顺序表示及常用操作
数据结构笔记目录：数据结构与算法（一）—— 线性表的顺序表示及常用操作数据结构与算法（二）—— 线性表的链式表示及常用操作数据结构与算法（三）—— 线性表的应用数据结构与算法（四）—— 栈和队列数据结构与算法（五）—— 串、数组和广义表数据结构与算法（六）—— 数和二叉树 顺序表的构建12345#define max_Size 100typedef struct{ ElemType elem[max_Size]; int length;//当前长度}SqList; Ex:112345678910#define max_Size 100 //宏定义最大长度typedef struct{ char ISBN[20]; char name[50]; float price;}Book;typedef struct SqList{ Book* add;//存储空间基地址 int...
2025-02-02
稀疏多项式的运算非伪码完整实现
伪码描述过于抽象，于是决定自己动手按照逻辑实现一次。看到AC的时候实在是太过激动，于是决定另开一篇文章分享一下实现源码。代码写的及其的不美观，要是能再精简一下就好了 12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788#include <iostream>using namespace std;typedef struct PNode{float coef; //系数int expn; //指数struct PNode* next; //指针域}PNode,*Polynomal;void MergeList_L(Polynomal LA,Polynomal LB,Polynomal &LC){ PNode* p = LA ->...
