数据结构笔记目录：

  1. 数据结构与算法（一）—— 线性表的顺序表示及常用操作
  2. 数据结构与算法（二）—— 线性表的链式表示及常用操作
  3. 数据结构与算法（三）—— 线性表的应用
  4. 数据结构与算法（四）—— 栈和队列
  5. 数据结构与算法（五）—— 串、数组和广义表
  6. 数据结构与算法（六）—— 数和二叉树

树的相关定义

  • 根节点：非空树中无前驱结点的结点
  • 结点的度：结点拥有的子树数量
  • 树的度：树内各节点的最大度
  • 叶子：度等于零的终端节点
  • 孩子与双亲：结点的子树的根称为该结点的孩子，该结点称为孩子的双亲
  • 祖先：从根到该结点所经分支上的所有结点
  • 有序树：将树中每个结点的各子树看成是从左到右有次序的(即不能互换)
  • 无序树：将树中每个结点的各子树从左到右是没有次序的(即可以互换)

二叉树的性质

  1. 在二叉树的第i层上至多有$2^{i-1}$个结点
  2. 深度为k的二叉树至多有$2^{k}-1$个结点
  3. 对于任何一颗二叉树T，如果其叶子数为$n_{0}$，度为2的结点数为$n_{2}$，则$n_{0} = n_{2} +1$
    对于完全二叉树：
  4. 具有n个结点的完全二叉树的深度为$\lfloor log_2(n) \rfloor$
  5. 对于某一编号为i的结点，它的双亲结点必为$\lfloor i/2 \rfloor$，左右孩子分别为2i、2i+1

满二叉树与完全二叉树：可以用顺序存储结构还原的树

满二叉树：深度为k，且有$2^{k}-1$个结点

完全二叉树：深度为k，每一个结点都与深度为k的满二叉树中编号为1-n的结点一一对应

特点：

  1. 叶子只可能分布在层次最大的两层
  2. 对任一结点，如果其右子树的最大层次为i，左子树的最大层次必定为i或者i+1

二叉树的存储结构

二叉树的顺序存储结构

一般只适用于存放满二叉树和完全二叉树

1
2
#define max_Size = 100
typedef int SqBiTree[max_Size];

二叉树的链式存储结构

二叉链表

1
2
3
4
5
typedef struct BiNode{
    ElemType data;
    struct BiNode* lchild;
    struct BiNode* rchild;
}BiNode,*BiTree;

空指针数目 = 2n - (n-1) = n + 1

解释：n个结点会产生2n个指针域。除去头结点剩下均为孩子节点，均需要被存放在指针域，故需要占用n-1个指针域。
则空指针数目为：2n - (n -1) = n + 1

三叉链表

1
2
3
4
5
6
typedef struct TriTNode{
    ElemType data;
    struct TriTNode* lchild;
    struct TriTNode* rchild;
    struct TriTNode* parent;
}TriTNode,*TriTree;

遍历二叉树和搜索二叉树

遍历二叉树

遍历二叉树的三种顺序：

  1. 先序遍历（根左右）
  2. 中序遍历（左根右）
  3. 后序遍历（左右根）

Ex:1

例：求下图所示二叉树的三种遍历顺序
图5.1.1-1 二叉树

先序遍历：ABDGCEHF
中序遍历：DGBAEHCF
后序遍历：GDBHEFCA

由遍历序列确定二叉树：先序和后序不能确定唯一序列

  1. 先序竖着摆放，中序横着摆放，画表格。画完表格后：
  • 找最高点M
  • 在最高点M左边的区域内找最高点L
  • 在最高点M右边的区域内找最高点R
  • 连接L-M-R
  • 用L取代M，递归下去，用R取代M，递归下去
  1. 后序竖着、倒着摆放，中序横着摆放，画表格。

遍历二叉树算法实现

  1. 先序遍历二叉树
    1
    2
    3
    4
    5
    6
    7
    void PreOrderTraverse(BiTree T){
      if(T!=NULL){
        print(T.data);
        PreOrderTraverse(T.lchild);
        PreOrderTraverse(T.rchild);
      }
    }
  2. 中序遍历二叉树
    1
    2
    3
    4
    5
    6
    7
    void InOrderTraverse(BiTree T){
      if(T!=NULL){
        InOrderTraverse(T.lchild);
        print(T.data);
        InOrderTraverse(T.rchild);
      }
    }
  3. 后序遍历二叉树
    1
    2
    3
    4
    5
    6
    7
    void PoseOrderTraverse(BiTree T){
      if(T!=NULL){
        PostOrderTraverse(T.lchild);
        PostOrderTraverse(T.rchild);
        print(T.data);
      }
    }

    如果去掉输出语句，从递归的角度看，三种算法是完全相同的，或说这三种算法的访问路径是相同的，只是访问结点的时机不同
    从虚线的出发点到终点的路径上，每个结点经过3次
    图5.1.3-1 遍历路径示意图

    第1次经过时访问=先序遍历
    第2次经过时访问=中序遍历
    第3次经过时访问=后序遍历

    算法分析：
  4. 时间复杂度O(n) //每个结点只访问一次
  5. 空间复杂度O(n) //栈占用的最大辅助空间

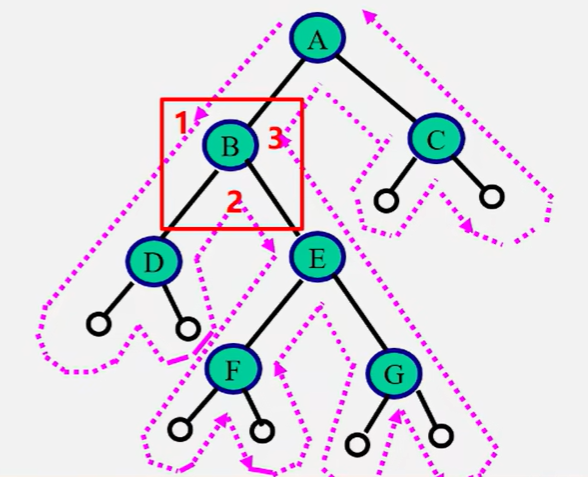
中序遍历的非递归算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void InOrderTraverlverse(BiTree T){
  BiNode* p = T;//p指针指向当前操作元素
  BiNode* q;
  InitStack(S);//初始化一个栈S
  if(p!=NULL&&StackEmpty(S) != 1){
      if(p){
        Push(S,p);//根节点进栈，继续遍历左子树
      }
      else{
        Pop(S,q);
        print(q->data);
        p = q -> rchild;//当左子树为空，访问根节点并出栈，遍历右子树
      }
  }
}

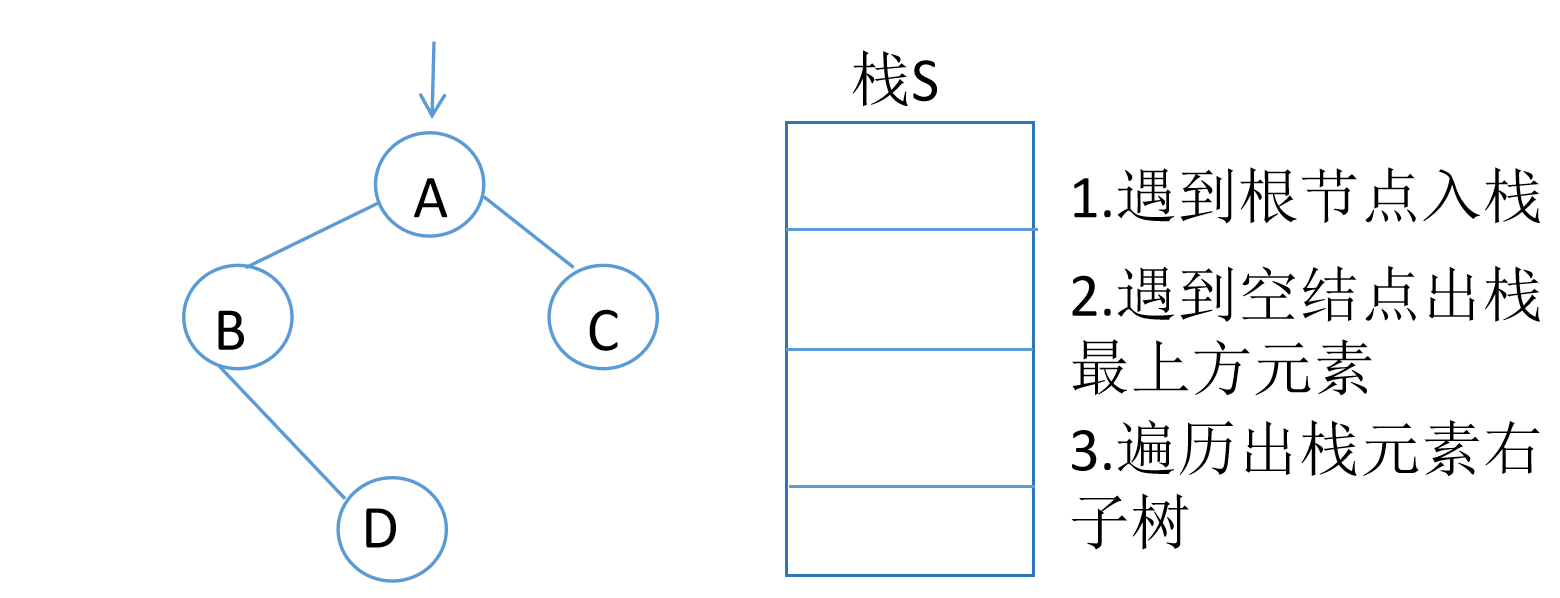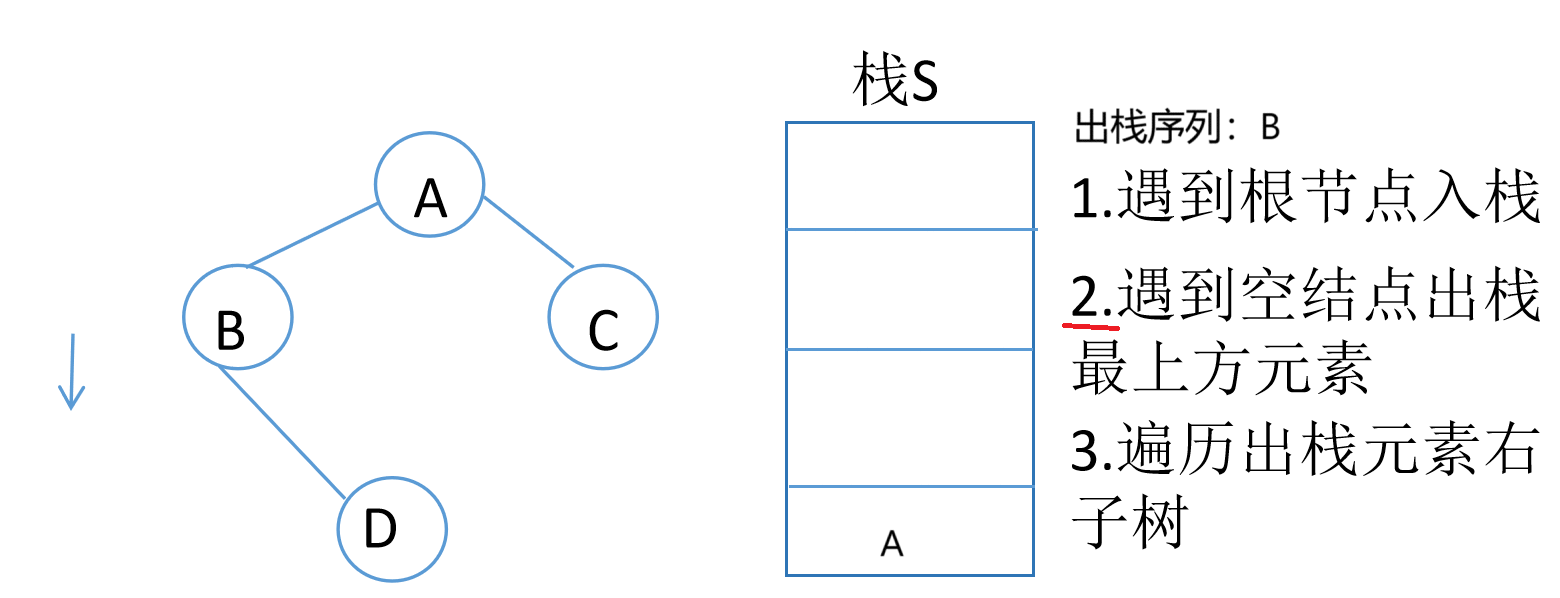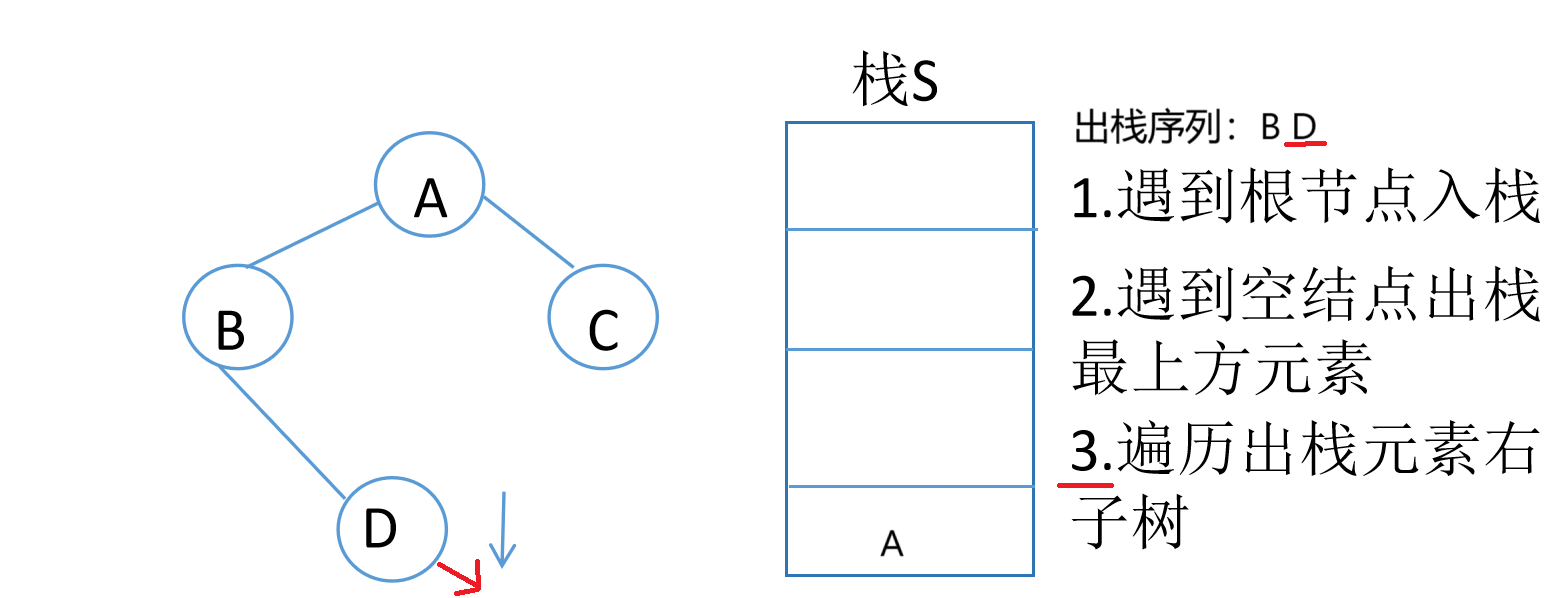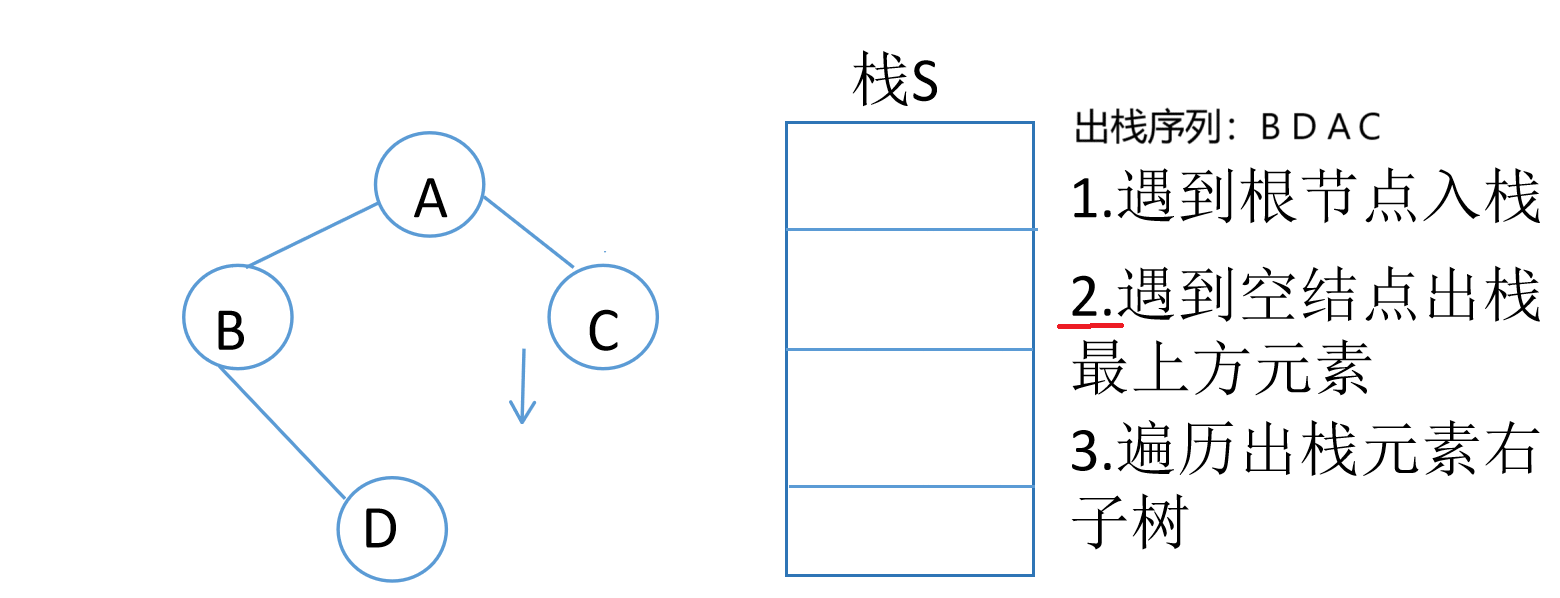
图5.2-1 中序遍历的非递归算法动画演示

二叉树的层次遍历（广度优先搜索）

  1. 创建一个队列，根节点入队
  2. 队列非空时出队一个元素，同时将其左右孩子入队
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    void LevelOrder(BtNode *b){ //传入二叉树根节点
      BTNode *p; //用于存放出队元素
      SqQueue *qu; //用于存放结点的队列
      InitQueue(qu);
      enQueue(qu,b); //将根节点存入队列
      while(!QueueEmpty(qu)){
        deQueue(qu,p); //出队结点p
        printf(p->data) //访问p结点
        while(p->lchild != NULL) enQueue(qu,p->lchild) //有左孩子入队左孩子
        while(!p->rchild != NULL) enQueue(qu,p->rchild) //有右孩子入队右孩子
      }
    }

二叉树的建立：以先序遍历为序

先序遍历不能唯一确定树，故输入时利用#代表空结点以保证所建立的树唯一

1
2
3
4
5
6
7
8
9
10
11
int CreateBiTree(BiTree &T){
  cin >> ch;
  if(ch=="#") T = NULL; //如果输入为#则证明该结点为空
  else{
  T = (BiTNode *)malloc(sizeof(BiTNode));
  T -> data = ch; //生成根节点
  CreateBiTree(T -> lchild); //构造左子树
  CreateBiTree(T -> rchild); //构造右子树
  }
  return 1;
}